Abbildungen

Eine der wichtigsten Relationen überhaupt stellen die Abbildungen da. Sie tauchen überall in der Mathematik auf und in der Realität lassen sich viele Probleme durch diese speziellen Relationen darstellen.

Funktionen

Bevor wir uns den Abbildungen widmen, definieren wir die Eindeutigkeit:

Eindeutigkeit

Eine Relation $R \subseteq A \times B$ ist eindeutig, wenn

$$\forall x \in A\ \forall y, y' \in B:\ (x,y) \in R \wedge (x,y') \in R \rightarrow y = y'$$

Anschaulich gesprochen heißt das, dass von jedem $x$, das in der Relation $R$ vorkommt, nur ein Pfeil weggeht. Gegeben seien $A = \{1, 2, 3, 4, 5\}$, $B = \{a, b, c, d\}$ und $R = \{(1,a), (1,d), (2,b), (3,b), (4,d)\} \subseteq A \times B$. $R$ ist nicht eindeutig, da $(1,a)$ und $(1,d)$ vorkommen. Laut Definition muss aber $y=y'$ gelten, wenn $x$ in $R$ enthalten, aber es gilt $a \ne d$. Durch entfernen einer dieser Komponenten, z.B. $(1,d)$ wird $R$ eindeutig. Im folgenden Schaubild ist links das ursprüngliche $R$ zu sehen, bei dem von der $1$ zwei Pfeile abgehen. Rechts ist dann die eindeutige Relation, da von der linken Seite maximal ein Pfeil pro Element abgeht. Bei der Eindeutigkeit ist es egal, wie viele Pfeile rechts auf ein Element zugehen, es geht nur um die linke Seite.

Abbildung / Funktion

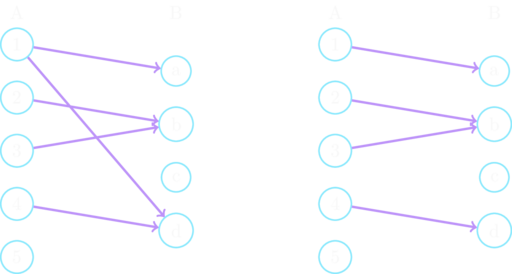
$f$ ist Abbildung oder Funktion von $A$ in $B$ $:=$

• $f$ ist Relation, also $f \subseteq A \times B$
• $D(f) = A$, also $f$ ist Relation von $A$ in $B$
• $f$ ist eindeutig

Mathematisch-logisch aufgeschrieben:

$$\forall x \in A\ \exists ! y \in B:\ (x,y) \in A \times B$$

Man schreibt dafür: $f:\ A \rightarrow B$.
Statt $R(x) = \{y\}$ wie bei normalen Relationen, schreibt man verkürzt $f(x) = y$, da das $y$ ja nun eindeutig ist.

Eine Funktion ordnet also jedem Element aus $A$ genau ein $y$ aus $B$ zu.

In der Analysis und auch in anderen mathematischen Gebieten findet man häufig eine alternative textliche Einführung:

Alternative Definition

Eine Abbildung oder eine Funktion einer Menge $A$ in eine Menge $B$ ordnet jedem Element $x \in A$ genau ein Element $y \in B$ zu.

Bei dieser Definition wird komplett auf die mengentheoretische Begriffe wie geordnetes Paar oder auch Relation verzichtet. Erst aufbauend darauf wird dann mengentheoretisch der Graph der Funktion definiert als $G_f := \{(x,f(x))\ |\ x \in A \wedge f(x) \in B\} \subseteq A \times B$. Aus mengentheoretischer Sicht stimmen in diesen Fällen die Begriffe "Funktion" und "Graph der Funktion" überein.

Beispiele

Gegeben seien $A = \{1, 2, 3, 4, 5\}$ und $B = \{a, b, c, d\}$. Eine Abbildung $f:\ A \rightarrow B$ können dann sein:

• $f = \{(1,b)\}$
• $f = \{(1,a), (2,b), (3,b), (4,d)\}$
• $f = \{(1,b), (2,c), (3,d), (4,a), (5,b)\}$
• ...

Wenn man eine rechnerische Vorschrift (Abbildungsvorschrift) angeben möchte, wie ein $y$ zu einem $x$ berechnet werden soll, dann schreibt man Abbildungen so:

Schreibweisen

$$f:\ A \rightarrow B,\ x \mapsto f(x) \qquad\qquad\text{oder}\qquad\qquad f: \begin{cases} A \rightarrow B\\ x \mapsto f(x) \end{cases}$$

wobei anstelle $f(x)$ dann z.B. eine Funktionsgleichung tritt.

Beispiele

• $f:\ \mathbb{R} \rightarrow \mathbb{R},\ x \mapsto x^2 \quad$ für eine Parabel
• $f: \begin{cases} \mathbb{N} \rightarrow \mathbb{R}\\ x \mapsto \sqrt{x} \end{cases} \quad$ für Wurzeln von natürlichen Zahlen

Es werden noch mehr unterschiedliche Darstellungsformen für Funktionen auftauchen, je nachdem wie es gerade angebracht ist. Bis dahin sollten einem die Begriffe allerdings so vertraut vorkommen, dass eine genaue Definition oder Einführung nicht notwendig ist.

Grundlegende Eigenschaften von Funktionen

Die Verkettung, oder auch Komposition, $f \circ g: A \rightarrow C$ von Funktionen $f:\ A \rightarrow B$ und $g:\ B \rightarrow C$ ist wieder eine Funktion. Für die Komposition gilt $f \circ g = g(f(x))$. In anderer Literatur kann es sein, dass die Komposition anders definiert ist und dann $f \circ g = f(g(x))$ gilt.

Jedoch ist das Inverse $f^{-1}$ einer Funktion $f$ im Allgemeinen keine Funktion mehr.

Zwei Funktionen $f$ und $g$ sind gleich $f=g$, wenn für alle $x$ gilt $f(x) = g(x)$.

Injektivität, Surjektivität, Bijektivität

Sei $f: A \rightarrow B$ eine Funktion.

• $f$ heißt injektiv (eineindeutig) $:=\ \forall x,x' \in A:\ f(x) = f(x') \rightarrow x = x'$
• $f$ heißt surjektiv (Abbildung auf $B$) $:=\ \forall y \in B\ \exists x \in A:\ f(x) = y$
• $f$ heißt bijektiv (eineindeutige Abbildung auf $B$) $:=\ f$ ist injektiv und surjektiv

Injektivität bedeutet, dass jedes $y$ aus der Bildmenge höchstens einmal abgebildet wird. Es würden in einem Schaubild also keine zwei oder mehr Pfeile auf ein $y \in B$ treffen. Surjektivität bedeutet, dass die Bildmenge die gesamte Menge $B$ umfasst, dass also $W(f) = B$ gilt. Siehe hierzu auch die Definition von Relationen auf einer Menge. Bijektivität schließlich bedeutet, dass jedes Element $x \in A$ auf genau ein Element $y \in B$ abgebildet wird und, dass jedes $y \in B$ "belegt" ist.

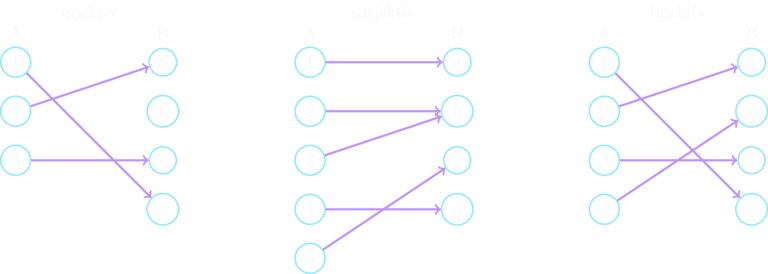
Im Schaubild ist zu erkennen, wie bei der Injektivität kein Element aus $B$ mehr als ein mal von einem Pfeil getroffen wird. Es ist möglich, dass ein Element aus $B$ gar nicht getroffen, aber eben nie mehr als ein mal. Bei Surjektivität ist zu sehen, wie kein Element aus $B$ frei bleibt. Hier ist es möglich, dass mehr als ein Pfeil auf ein Element aus $B$ geht. Es muss also mindestens ein Pfeil eingehen. In dem Schaubild zur Bijektivität, als Kombination aus Beidem, ist zu sehen, dass jedes Element von $B$ genau ein mal von einem Pfeil getroffen wird. Es darf also kein Element aus $B$ frei bleiben und es darf nur genau ein Pfeil pro Element eingehen.

Dass dabei $A$ und $B$ gleich viele Elemente haben müssen ist kein Zufall. Welche Rolle bijektive Abbildungen bei der Kardinalität ("Größe") von Mengen haben, wird im Kapitel Endlichkeit und Kardinalzahlen erklärt.

Beispiele

Gegeben sei $f:\ \mathbb{N} \rightarrow \mathbb{N},\ n \mapsto f(n)$. Betrachten verschiedene Funktionsgleichungen für $f(n)$:

• $f(n)\ :=\ n+1 \quad$ (Nachfolgerfunktion) ist injektiv, aber nicht surjektiv, da $0 \notin W(f)$
• $f(n)\ := \begin{cases} \lfloor \frac{n}{2} \rfloor & n \text{ gerade}\\ 0 & n \text{ ungerade} \end{cases} \quad$ ist surjektiv, aber nicht injektiv, da z.B. $f(1) = f(3) = 0$
• $f(n)\ :=\ n \quad$ (identische Abbildung) ist injektiv, surjektiv und damit auch bijektiv

Gegeben sei $f:\ \mathbb{R} \rightarrow \mathbb{R},\ x \mapsto x^2$, also eine Parabelfunktion. $f$ ist weder injektiv, noch surjektiv. Wenn man allerdings die Abbildungsmengen einschränkt, kann man eine injektive, surjektive oder bijektive Abbildung erhalten. Im Folgenden bezeichnen wir $\mathbb{R}_{\ge 0}$ als die Menge der nicht-negativen reellen Zahlen, also reelle Zahlen $\ge 0$. Am einfachsten ist es, sich die folgenden Fälle zu skizzieren:

• $f:\ \mathbb{R}_{\ge 0} \rightarrow \mathbb{R},\ x \mapsto x^2 \quad$ ist injektiv, aber nicht surjektiv
• $f:\ \mathbb{R} \rightarrow \mathbb{R}_{\ge 0},\ x \mapsto x^2 \quad$ ist surjektiv, aber nicht injektiv
• $f:\ \mathbb{R}_{\ge 0} \rightarrow \mathbb{R}_{\ge 0},\ x \mapsto x^2 \quad$ ist injektiv und surjektiv und damit auch bijektiv

Zu bijektiven Funktion sagt man auch, sie bilden "umkehrbar eindeutig" ab. Eingangs wurde erwähnt:

Jedoch ist das Inverse $f^{-1}$ einer Funktion $f$ im Allgemeinen keine Funktion mehr.

Im Falle einer bijektiven Abbildung $f$ ist $f^{-1}$ allerdings eine Abbildung und man nennt diese dann Umkehrabbildung oder Umkehrfunktion.

Beispiele

Bei einer bijektiven Abbildung, die durch eine Funktionsgleichung $y = f(x)$ gegeben ist, kann man die Umkehrabbildung einfach dadurch berechnen, dass man die Funktionsgleichung nach $x$ umstellt. Man hat dann einen Ausdruck der Form $x = g(y) = f^{-1}(y)$.

Gegeben sei die Abbildung $f:\ \mathbb{R} \rightarrow \mathbb{R}^+$ mit der Funktionsgleichung $f(x) = e^x$. Die Exponentialfunktion ist surjektiv, wenn man diese auf die positiven reellen Zahlen abbildet, also die nicht-negativen reellen Zahlen ohne die $0$: $\mathbb{R}^+ := \mathbb{R}_{>0} = \mathbb{R}_{\ge 0} \setminus \{0\}$. Der ganze Beweis der Bijektivität sei an dieser allerdings weggelassen.

Die Umkehrfunktion $f^{-1}:\ \mathbb{R}^+ \rightarrow \mathbb{R}$ kann man nun durch Umstellen nach $y$ berechnen:

$$\begin{alignat*}{2} && y &= f(x)\\ && y &= e^x\\ && \ln y &= \ln e^x\\ && \ln y &= x\\ \Longrightarrow \quad && f^{-1}(y) &= \ln y \end{alignat*}$$

Erweiterung von Abbildungen

Gegeben seien $S$ als die Menge aller Schulkinder und $K$ als die Menge aller Klassen einer Schule. Als Abbildung definieren $k: S \rightarrow K$, die jedem Schulkind die eigene Klasse zuordnet. Der Direktor hat nun eine Liste von Schulkindern, mit denen er zusammen sprechen möchte. Doch möchte er nicht in jede einzelne Klasse gehen, um ein Schulkind abzuholen, sondern nur in die Klassen, in denen auch ein Schulkind von der Liste ist. In diesem Beispiel nehmen wir an, der Direktor kann die Liste in einem Computer eintippen und dieser gibt dann die Klassen aus, in denen sich die Schulkinder befinden. Wir haben also eine Teilmenge von Schulkindern und bilden diese auf eine Teilmenge der Klassen ab. Durch diese Fragestellung haben wir die Abbildung $k$ auf ihre Potenzmenge erweitert.

Die Umkehrung der Fragestellung ist auch möglich: Der Direktor hat eine Liste von Klassen und möchte nun wissen, welche Schulkinder zu diesen Klassen gehören.

Formal lässt sich das so auffassen:

Erweiterung

Gegeben seien eine Abbildung $f:\ A \rightarrow B$ und die Teilmengen $X \subseteq A$ und $Y \subseteq B$.

$\widehat{f}(X)\ :=\ \{ y\ |\ y \in B \wedge \exists x \in X:\ f(x) = y \}$ heißt Erweiterung von $f$ auf $\mathcal{P}(A)$.

$\widehat{f^{-1}}(Y)\ :=\ \{ x\ |\ x \in A \wedge f(x) \in Y \}$ heißt Erweiterung von $\underbrace{f^{-1}}_{\substack{\text{Inverse Relation}\\\text{i.A. keine Abbildung}}}$ auf $\mathcal{P}(B)$.

$\widehat{f}:\ \mathcal{P}(A) \rightarrow \mathcal{P}(B)$ ist wie $f$ wieder eine Abbildung. Während $f^{-1}$ hier allgemein die inverse Relation ist und damit keine (Umkehr-)Abbildung, ist $\widehat{f^{-1}}:\ \mathcal{P}(B) \rightarrow \mathcal{P}(A)$ allerdings immer eine Abbildung.

Häufig schreibt man statt $\widehat{f}$ auch wieder nur $f$ bzw. für $\widehat{f^{-1}}$ auch wieder $f^{-1}$. Eine Verwechslung ist ausgeschlossen, da die Abbildung $f$ ein Element entgegennimmt, während die Erweiterung von $f$ eine Menge entgegennimmt.

Beispiele

Gegeben sei $f:\ \{1, 2, 3\} \rightarrow \{a, b, c, d\}$ mit $f(1) = a,\ f(2) = c,\ f(3) = a$. Dann sind bspw.:

• $\widehat{f}(\emptyset) = f(\emptyset) = \emptyset$
• $\widehat{f}(\{1, 2\}) = f(\{1, 2\}) = \{ a, c \}$
• $f(\{3\}) = \{ a \}$
• $f(\{1, 2, 3\}) = f(D(f)) = \{ a, b, c, d \} = W(f)$

und

• $\widehat{f^{-1}}(\emptyset) = f^{-1}(\emptyset) = \emptyset$
• $\widehat{f^{-1}}(\{a\}) = f^{-1}(\{a\}) = \{ 1 \}$
• $\widehat{f^{-1}}(\{b, d\}) = f^{-1}(\{b, d\}) = \emptyset$
• $f^{-1}(\{a, b, c, d\}) = f^{-1}(D(f^{-1})) = \{ 1, 2, 3 \} = W(f^{-1})$

Operationen

Im Kapitel Kartesisches Produkt wurde bereits die kartesische Potenz eingeführt. Mit den kartesischen Potenzen führen wir nun eine weitere wichtige Klasse von Abbildungen ein, die Operationen oder Verknüpfungen. Diese spielen in der Algebra eine wichtige Rolle.

Operation oder Verknüpfung

$f$ heißt innere $n$-stellige algebraische Operation $:=\ f:\ A^n \rightarrow A$.

Eine Operation ist also eine $A^{n+1}$-Relation.

Es gibt auch äußere Verknüpfungen, davon gibt es aber zwei unterschiedliche Arten. Diese werden zu späteren Zeitpunkten sinnvoll eingeführt.

$2$-stellige Relationen heißen auch binäre Relationen. Entsprechend heißen $2$-stellige Operationen auch binäre Operation. Bereits im Kapitel Verband wurden zweistellige Operationen das erste Mal genannt.

Beispiele

Aus dem Kapitel Verband wissen wir, dass $\cap$ und $\cup$ zweistellige Operationen für eine Menge $A$ sind:

• $\cap:\ \mathcal{P}^2(A) \rightarrow \mathcal{P}(A)$
• $\cup:\ \mathcal{P}^2(A) \rightarrow \mathcal{P}(A)$

Weitere Beispiele:

• $+:\ \mathbb{N}^2 \rightarrow \mathbb{N}$ als Addition in den natürlichen Zahlen: $+(a, b) = a+b \quad = \quad c$
  • $+(2,3) = 2 + 3 \quad = \quad 5$
  • $100 + 1 = 101$
• $\hat{\ }:\ \mathbb{R}^2 \rightarrow \mathbb{R}$ als Potenz: $\hat{\ }(a,b) = a^b \quad = \quad c$
  • $\hat{\ }(2,2) = 2^2 \quad = \quad 4$
  • $3^4 = 81$
• $\circ:\ \text{Abb}(A,A)^2 \rightarrow \text{Abb}(A,A)$ als Komposition: $\circ(f,g) = f \circ g = g(f(x)) \quad = \quad h$
  $\text{Abb}(A,A)$ ist dabei die Menge aller Abbildungen von $A$ in $A$.
  • Mit $f(x) = x^2,\ g(x) = x+2$ ist $\circ(f,g) = f \circ g = g(f(x)) \quad = \quad g(x^2) = x^2+2$
  • Mit $f(x) = \ln(x) + \frac{\pi}{2},\ g(x) = \sin x$ ist $$\begin{align*} \circ(f,g) = f \circ g = g(f(x)) &= g(\ln(x) + \frac{\pi}{2})\\ &= \sin\left( \ln(x) + \frac{\pi}{2} \right)\\ &= \cos(\ln(x)) \end{align*}$$